133. Clone Graph 克隆图

作者： 负雪明烛 id： fuxuemingzhu 个人博客： http://fuxuemingzhu.cn/

---

@TOC

题目地址：https://leetcode.com/problems/clone-graph/

题目描述

Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

Example:

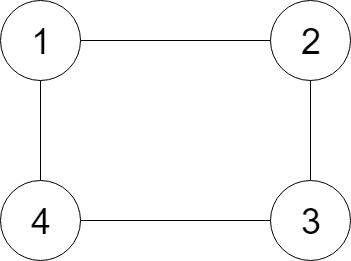
Input:

{"$id":"1","neighbors":[{"$id":"2","neighbors":[{"$ref":"1"},{"$id":"3","neighbors":[{"$ref":"2"},{"$id":"4","neighbors":[{"$ref":"3"},{"$ref":"1"}],"val":4}],"val":3}],"val":2},{"$ref":"4"}],"val":1}

Explanation:
Node 1's value is 1, and it has two neighbors: Node 2 and 4.
Node 2's value is 2, and it has two neighbors: Node 1 and 3.
Node 3's value is 3, and it has two neighbors: Node 2 and 4.
Node 4's value is 4, and it has two neighbors: Node 1 and 3.

Note:

1. The number of nodes will be between 1 and 100.
2. The undirected graph is a simple graph, which means no repeated edges and no self-loops in the graph.
3. Since the graph is undirected, if node p has node q as neighbor, then node q must have node p as neighbor too.
4. You must return the copy of the given node as a reference to the cloned graph.

题目大意

完全复制一个图结构。返回新的起始节点。

解题方法

DFS

这个题和138. Copy List with Random Pointer比较类似。至于图结构，我们可以使用DFS和BFS两种结构进行遍历。

一般的遍历只需要保存是否遍历过这个节点即可，但是由于这个题需要把neighboors对应复制过来。那么需要进行改进，改进的方式是把set改成dict，保存每个老节点对应的新节点是多少。在Python中，字典直接保存对象（指针）之间的映射。所以，我们直接把遍历过的对象和复制出来的对象一一对应即可。当我们遍历到一个新的节点的时候，需要判断这个节点是否在字典中出现过，如果出现过就把它对应的复制出来的对象放到其neighboors里，若没有出现过，那么就重新构造该节点，并把原节点和该节点放到字典中保存。

Python代码如下：

"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, neighbors):
        self.val = val
        self.neighbors = neighbors
"""
class Solution(object):
    def cloneGraph(self, node):
        """
        :type node: Node
        :rtype: Node
        """
        node_copy = self.dfs(node, dict())
        return node_copy
    
    def dfs(self, node, hashd):
        if not node: return None
        if node in hashd: return hashd[node]
        node_copy = Node(node.val, [])
        hashd[node] = node_copy
        for n in node.neighbors:
            n_copy = self.dfs(n, hashd)
            if n_copy:
                node_copy.neighbors.append(n_copy)
        return node_copy

C++代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;

    Node() {}

    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/
class Solution {
public:
    Node* cloneGraph(Node* node) {
        if (!node) return nullptr;
        if (m_.count(node))
            return m_[node];
        Node* node_copy = new Node(node->val, {});
        m_[node] = node_copy;
        for (Node* n : node->neighbors) {
            node_copy->neighbors.push_back(cloneGraph(n));
        }
        return node_copy;
    }
private:
    unordered_map<Node*, Node*> m_;
};

BFS

这个题同样也可以使用BFS解决。方法也是使用了字典保存每一个对应关系。当新构造出一个节点之后，必须同时把它放到字典中保存，这个很重要。另外就是每遍历到一个节点时，都要把它的所有邻居放到队列中。

python代码如下：

"""
# Definition for a Node.
class Node(object):
    def __init__(self, val, neighbors):
        self.val = val
        self.neighbors = neighbors
"""
class Solution(object):
    def cloneGraph(self, node):
        """
        :type node: Node
        :rtype: Node
        """
        que = collections.deque()
        hashd = dict()
        que.append(node)
        node_copy = Node(node.val, [])
        hashd[node] = node_copy
        while que:
            t = que.popleft()
            if not t: continue
            for n in t.neighbors:
                if n not in hashd:
                    hashd[n] = Node(n.val, [])
                    que.append(n)
                hashd[t].neighbors.append(hashd[n])
        return node_copy

C++代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;

    Node() {}

    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/
class Solution {
public:
    Node* cloneGraph(Node* node) {
        queue<Node*> q;
        q.push(node);
        unordered_map<Node*, Node*> m_;
        Node* node_copy = new Node(node->val, {});
        m_[node] = node_copy;
        while (!q.empty()) {
            Node* t = q.front(); q.pop();
            if (!t) continue;
            for (Node* n : t->neighbors) {
                if (!m_.count(n)) {
                    m_[n] = new Node(n->val, {});
                    q.push(n);
                }
                m_[t]->neighbors.push_back(m_[n]);
            }
        }
        return node_copy;
    }
};

日期

2019 年 3 月 9 日 —— 妇女节快乐