417. Pacific Atlantic Water Flow 太平洋大西洋水流问题
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/
题目地址: https://leetcode.com/problems/pacific-atlantic-water-flow/description/
题目描述
Given an m x n matrix of non-negative integers representing the height of each unit cell in a continent, the "Pacific ocean" touches the left and top edges of the matrix and the ``"Atlantic ocean"```touches the right and bottom edges.
Water can only flow in four directions (up, down, left, or right) from a cell to another one with height equal or lower.
Find the list of grid coordinates where water can flow to both the Pacific and Atlantic ocean.
Note:
- The order of returned grid coordinates does not matter.
- Both m and n are less than 150.
Example:
Given the following 5x5 matrix:
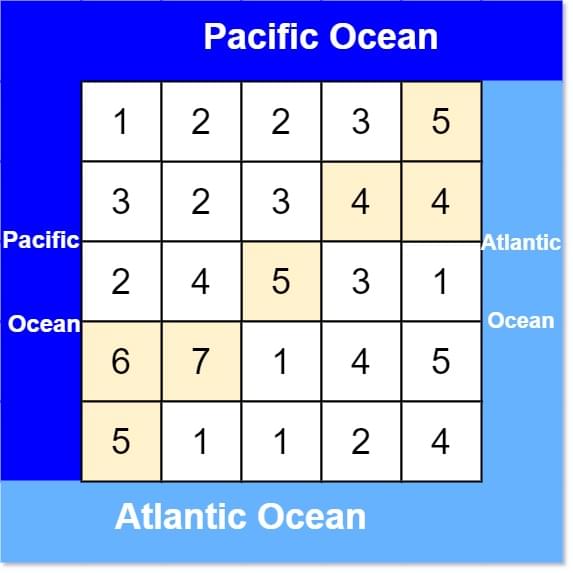
Return:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (positions with parentheses in above matrix).
题目大意
上面一条边和左边一条边代表的是太平洋,右边一条边和下边一条边代表的是大西洋。
现在告诉你水往低处流,问哪些位置的水能同时流进太平洋和大西洋?
解题方法
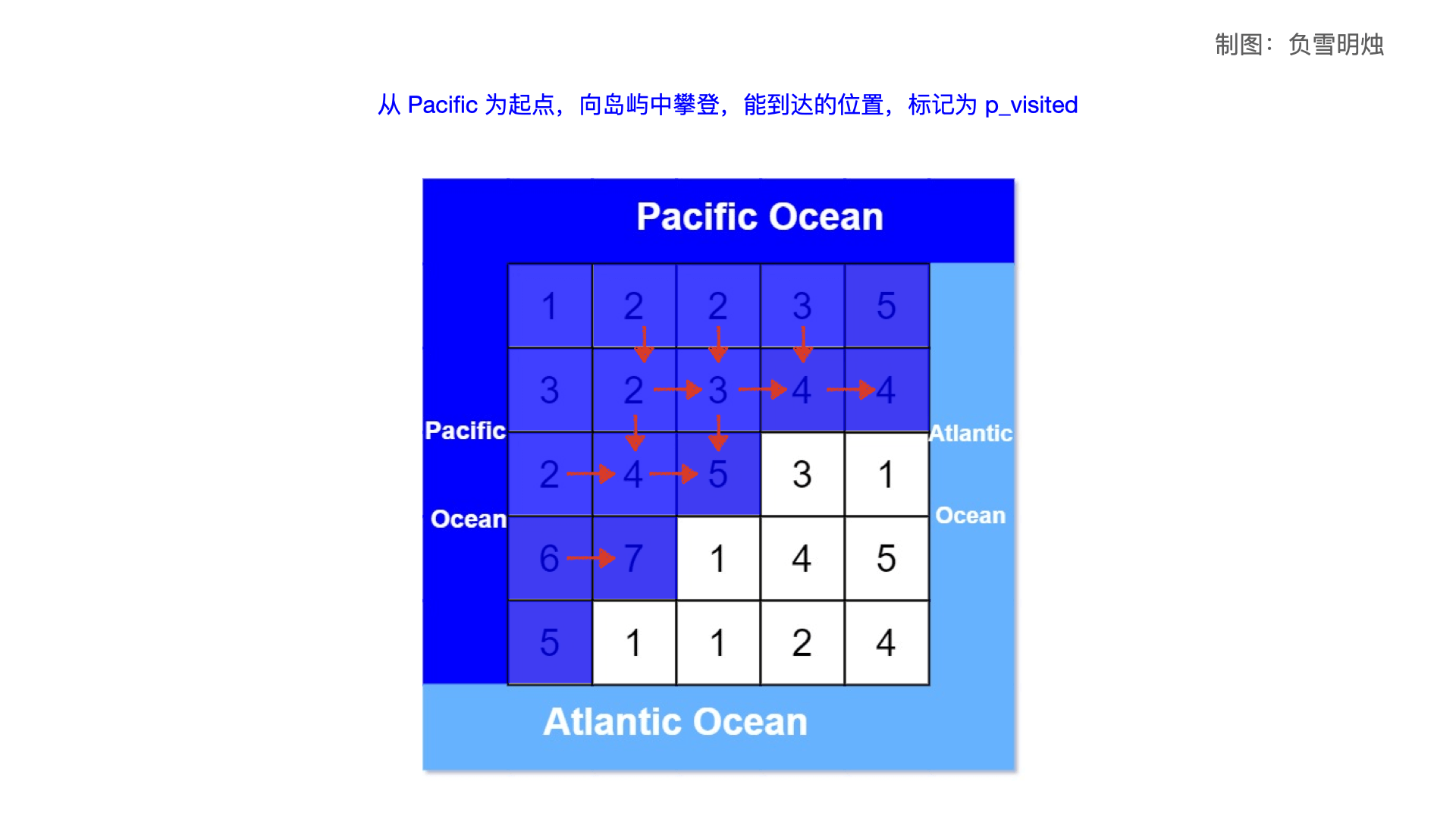
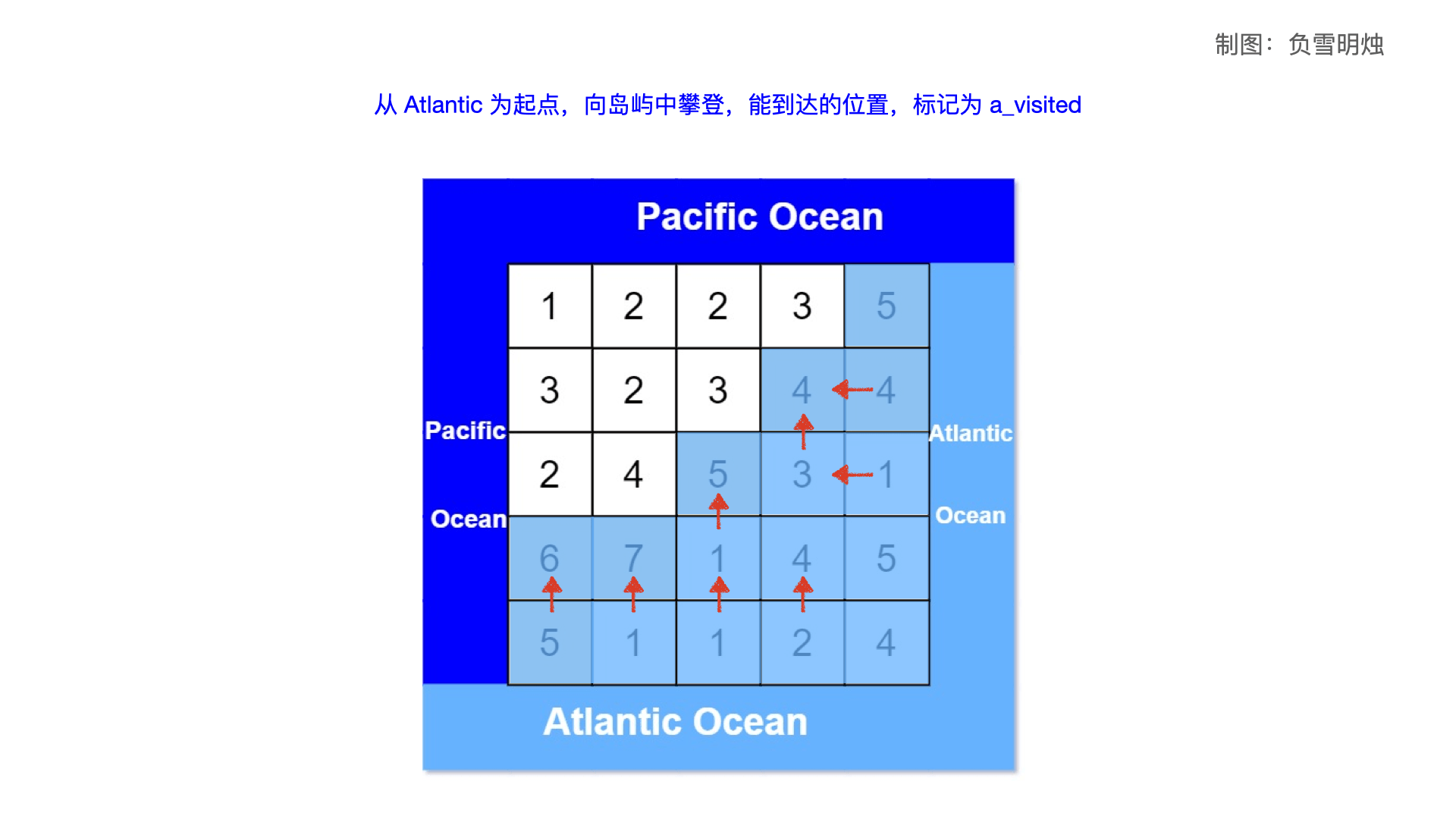
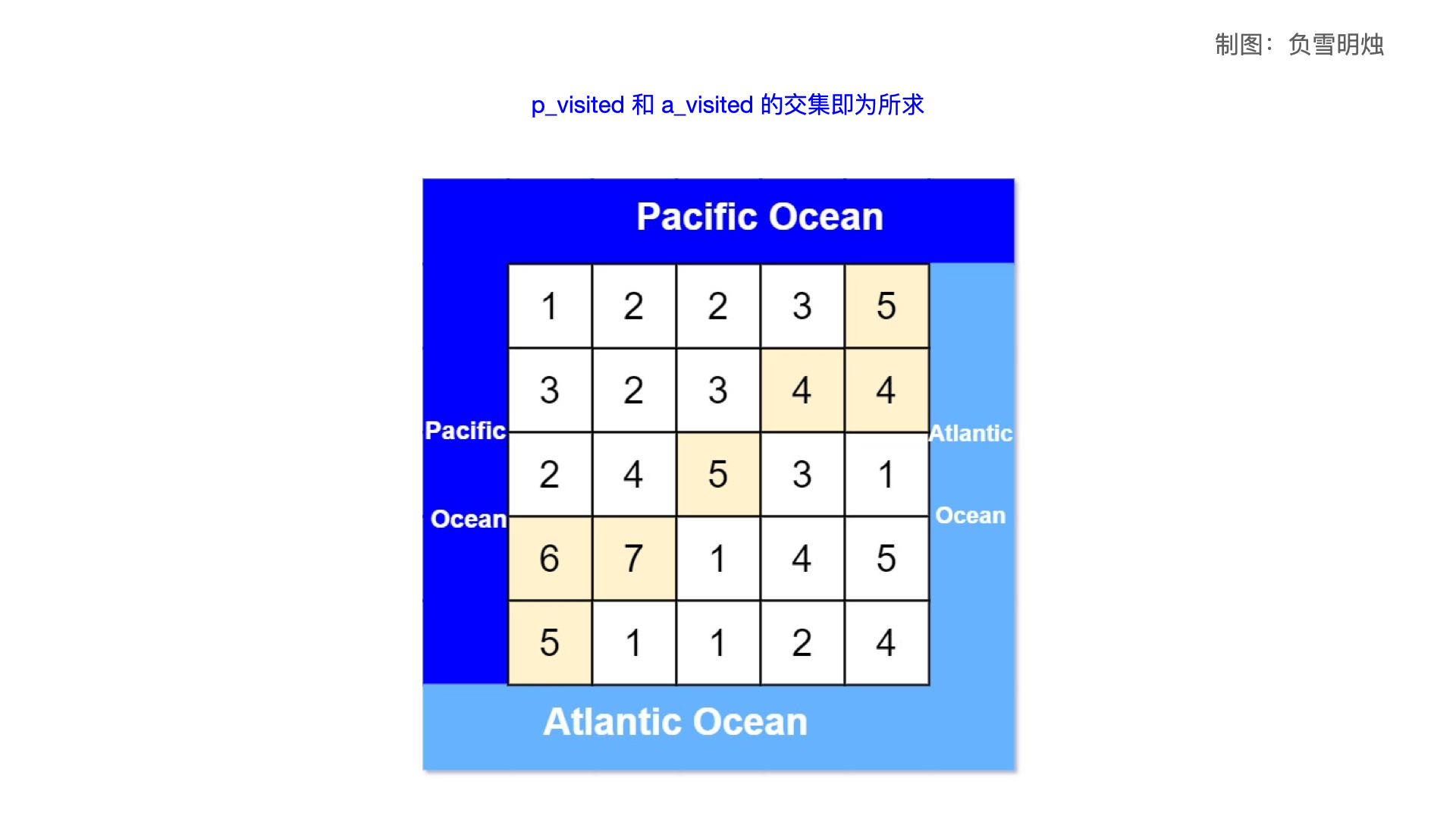
要解决的问题:哪些位置的雨水能同时流进太平洋和大西洋。 重要思路:将水的流向反转,假设太平洋和大西洋的水 从低向高 “攀登”,分别能到达哪些位置,分别用 p_visited 和 a_visited 表示。两者的交集就代表能同时流向太平洋和大西洋的位置。
DFS
直接DFS求解。一般来说 DFS 需要有固定的起点,但是对于本题,4 条边都是能与大洋接壤的,那么就把 4条边界的每个位置都算作 DFS 的起点 。
使用两个二维数组 p_visited 和 a_visited,分别记录太平洋和大西洋的水能从低向高“攀登”到的位置。
然后对 4 条边进行遍历,看以这些边的每个位置为起点,进行攀登;把能到达的哪些的位置,分别在 p_visited 和 a_visited标记出来。
注意了,因为是从边界向中间去“攀登”,所以,这个时候是新的点要比当前的点海拔高才行。
Python代码如下:
class Solution(object):
def pacificAtlantic(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[List[int]]
"""
if not matrix or not matrix[0]: return []
m, n = len(matrix), len(matrix[0])
p_visited = [[False] * n for _ in range(m)]
a_visited = [[False] * n for _ in range(m)]
for i in range(m):
self.dfs(p_visited, matrix, m, n, i, 0)
self.dfs(a_visited, matrix, m, n, i, n -1)
for j in range(n):
self.dfs(p_visited, matrix, m, n, 0, j)
self.dfs(a_visited, matrix, m, n, m - 1, j)
res = []
for i in range(m):
for j in range(n):
if p_visited[i][j] and a_visited[i][j]:
res.append([i, j])
return res
def dfs(self, visited, matrix, m, n, i, j):
visited[i][j] = True
directions = [(-1, 0), (1, 0), (0, 1), (0, -1)]
for dire in directions:
x, y = i + dire[0], j + dire[1]
if x < 0 or x >= m or y < 0 or y >= n or visited[x][y] or matrix[x][y] < matrix[i][j]:
continue
self.dfs(visited, matrix, m, n, x, y)
C++代码如下:
class Solution {
public:
vector<pair<int, int>> pacificAtlantic(vector<vector<int>>& matrix) {
if (matrix.empty() || matrix[0].empty()) return {};
const int M = matrix.size();
const int N = matrix[0].size();
vector<vector<bool>> p_visited(M, vector<bool>(N));
vector<vector<bool>> a_visited(M, vector<bool>(N));
for (int i = 0; i < M; ++i) {
dfs(matrix, p_visited, i, 0);
dfs(matrix, a_visited, i, N - 1);
}
for (int j = 0; j < N; ++j) {
dfs(matrix, p_visited, 0, j);
dfs(matrix, a_visited, M - 1, j);
}
vector<pair<int, int>> res;
for (int i = 0; i < M; ++i) {
for (int j = 0; j < N; ++j) {
if (p_visited[i][j] && a_visited[i][j]) {
res.push_back({i, j});
}
}
}
return res;
}
void dfs(vector<vector<int>>& matrix, vector<vector<bool>>& visited, int i, int j) {
const int M = matrix.size();
const int N = matrix[0].size();
visited[i][j] = true;
vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (auto d : dirs) {
int nx = i + d.first;
int ny = j + d.second;
if (nx >= 0 && nx < M && ny >= 0 && ny < N && !visited[nx][ny] && matrix[nx][ny] >= matrix[i][j]) {
dfs(matrix, visited, nx, ny);
}
}
}
};
最坏情况下的时间复杂度: 空间复杂度: 。
参考资料:
日期
2018 年 10 月 1 日 —— 欢度国庆!
