作者： 负雪明烛 id： fuxuemingzhu 个人博客： http://fuxuemingzhu.cn/

---

@TOC

题目地址：https://leetcode.com/problems/circular-array-loop/

题目描述

You are given a circular array nums of positive and negative integers. If a number k at an index is positive, then move forward k steps. Conversely, if it's negative (-k), move backward k steps. Since the array is circular, you may assume that the last element's next element is the first element, and the first element's previous element is the last element.

Determine if there is a loop (or a cycle) in nums. A cycle must start and end at the same index and the cycle's length > 1. Furthermore, movements in a cycle must all follow a single direction. In other words, a cycle must not consist of both forward and backward movements.

Example 1:

Input: [2,-1,1,2,2]
Output: true
Explanation: There is a cycle, from index 0 -> 2 -> 3 -> 0. The cycle's length is 3.

Example 2:

Input: [-1,2]
Output: false
Explanation: The movement from index 1 -> 1 -> 1 ... is not a cycle, because the cycle's length is 1. By definition the cycle's length must be greater than 1.

Example 3:

Input: [-2,1,-1,-2,-2]
Output: false
Explanation: The movement from index 1 -> 2 -> 1 -> ... is not a cycle, because movement from index 1 -> 2 is a forward movement, but movement from index 2 -> 1 is a backward movement. All movements in a cycle must follow a single direction.

Note:

1. -1000 ≤ nums[i] ≤ 1000
2. nums[i] ≠ 0
3. 1 ≤ nums.length ≤ 5000

Follow up:

Could you solve it in O(n) time complexity and O(1) extra space complexity?

题目大意

首先，要理解题目中的「环形数组」是什么。「环形数组」就是在逻辑上首尾相接的数组，即最后一个元素和第一个元素在逻辑上是相邻的（在物理存储上仍然是个普通的数组）。​

那么环形数组中存在循环是什么意思呢？这就是说，在环形数组中，每个位置存储的元素表示当前位置应该向前/向后移动的步数。如果在环形数组中绕了一圈又回到了原地，那么说明数组中存在循环。 ​

举个例子，在环形数组 [2, -1, 1, 2, 2] 中，存在循环：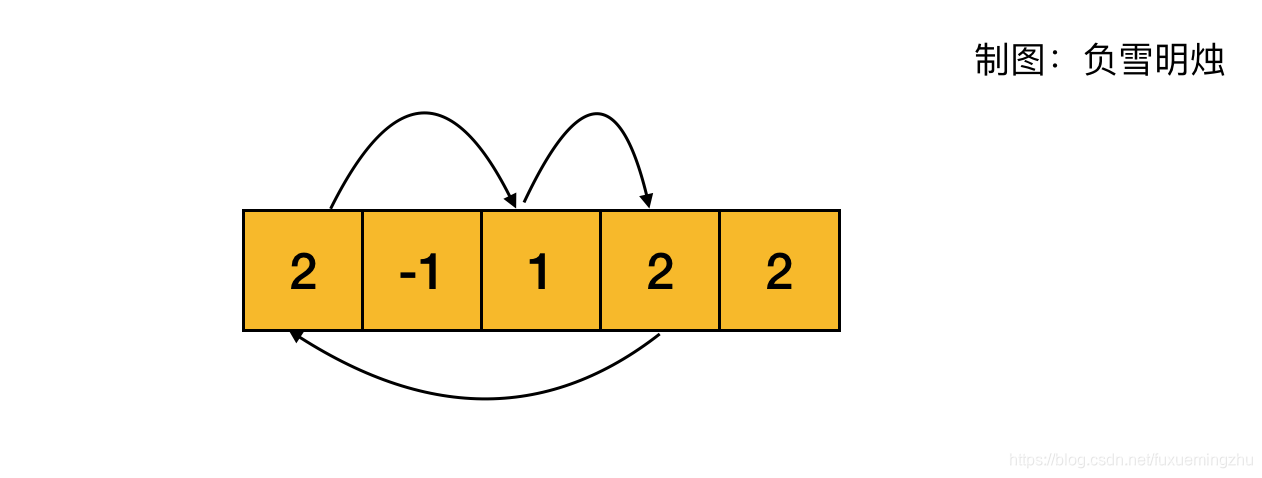

同时，题目约定了循环的条件： ​

• 所有 nums[seq[j]] 应当不是 全正 就是 全负，即只能沿着一个方向走。
• k > 1，即要求环的大小 > 1。

​

题目的示例 2 和 3 说明了上述循环的条件。 ​

示例 2 ，nums = [-1,2]，不算循环的原因是，循环中只有一个元素: ​

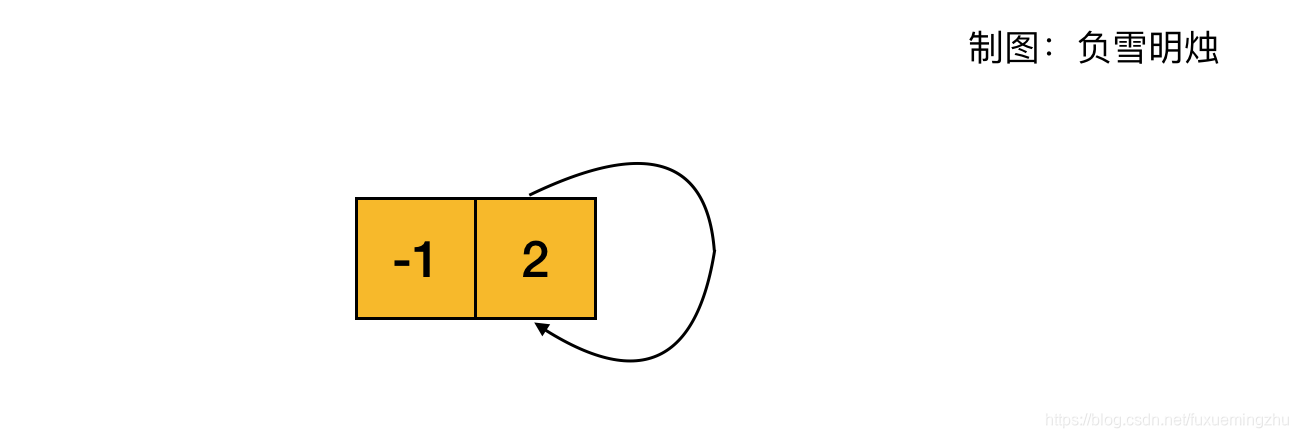
示例 3，nums = [-2,1,-1,-2,-2]，不算循环的原因是，循环中同时存在正、负数。 ​

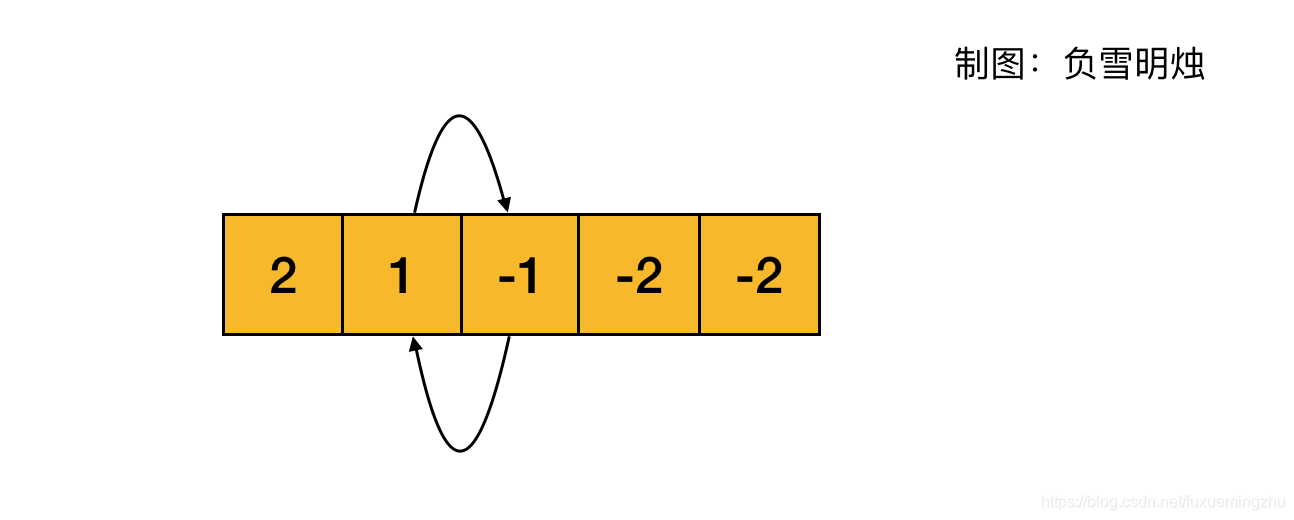
另外，需要提醒大家的是：循环的起点并不一定是位置 0.

解题思路

快慢指针

相信大家都做过「判断链表中是否有环」的题目，这两题的思路是一致的，常见的思路就是快慢指针，在链表问题中，快指针每次走 2 步，慢指针每次走 1 步。当快慢指针相遇的时候，说明存在环。​

在本题中，题目规定了数组中每个位置存储的元素就是每次需要移动的步数。所以快指针、慢指针每次走的步数等于 nums[fast]、nums[slow]；在每一次的移动中，快指针需要走 2 次，而慢指针需要走 1 次。当快慢指针相遇的时候，说明有环。 ​

起始时，让快指针先比慢指针多走一步，当两者在满足题目的两个限制条件的情况下，快满指针能够相遇，则说明有环。 ​

这个题难点在于题目的两个限制条件： ​

1. 在每次循环的过程中，必须保证所经历过的所有数字都是同号的。
   1. 那么，在快指针经历过的每个位置都要判断一下和出发点的数字是不是相同的符号。
2. 当快慢指针相遇的时候，还要判断环的大小不是 1。
   1. 所以，找到相遇点的位置后，如果再走 1 步，判断是不是自己。

​

下面的动图展示了在环形数组 [2, -1, 1, 2, 2] 中，如何利用快慢指针寻找判断环形数组中是否存在环。

​

​

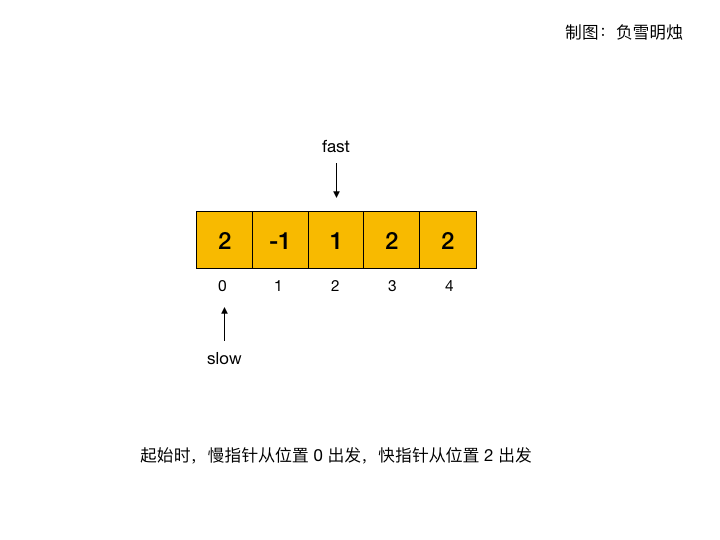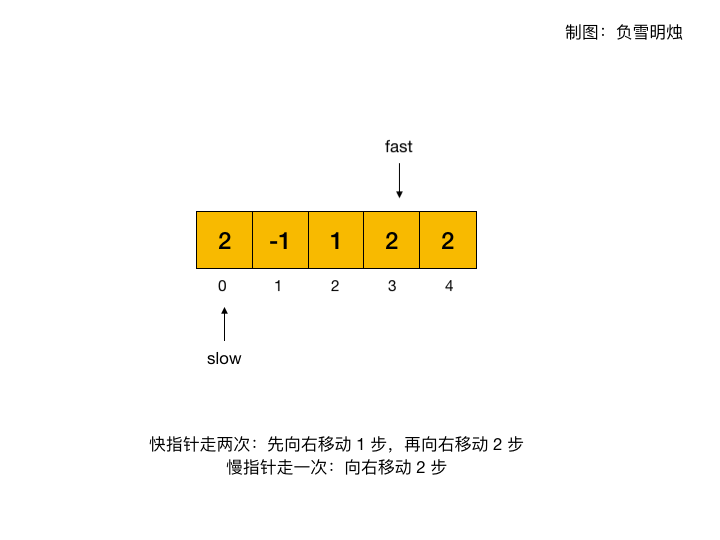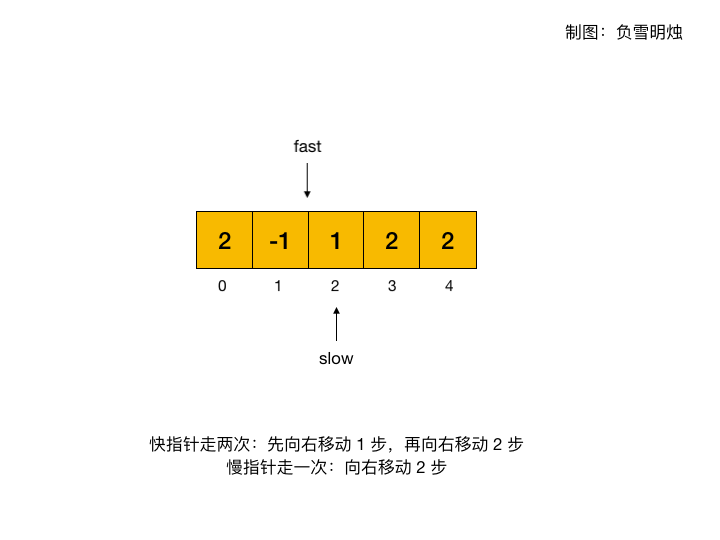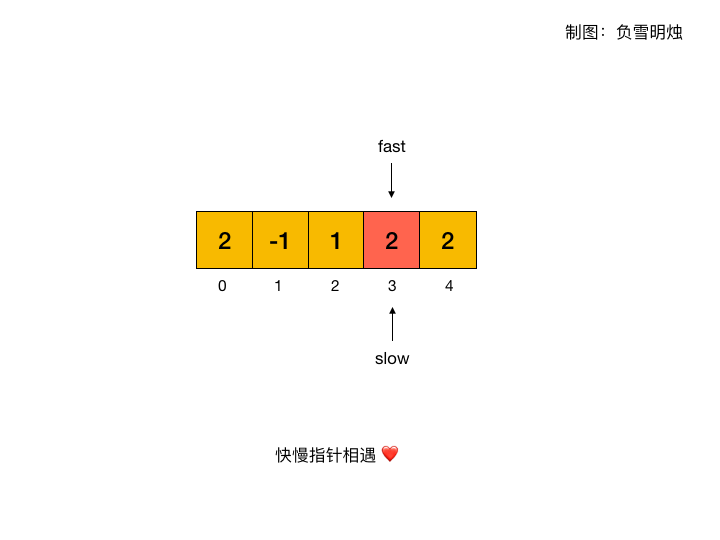
代码

在下面的代码中，我定义了一个 nextpos(index)的函数，用于判断每次移动后应该走到哪个位置。

Python代码如下：

class Solution(object):
    def circularArrayLoop(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """
        N, self.nums = len(nums), nums
        for i in range(N):
            slow = i
            fast = self.nextpos(slow)
            while nums[fast] * nums[i] > 0 and nums[self.nextpos(fast)] * nums[i] > 0:
                if fast == slow:
                    if slow == self.nextpos(slow):
                        break
                    return True
                slow = self.nextpos(slow)
                fast = self.nextpos(self.nextpos(fast))
        return False
    
    def nextpos(self, index):
        N = len(self.nums)
        return (index + self.nums[index] + N) % N

日期

2019 年 2 月 27 日 —— 二月就要完了 2021 年 8 月 7 日 —— 开始更新算法每日一题