480. Sliding Window Median 滑动窗口中位数

作者： 负雪明烛 id： fuxuemingzhu 公众号： 负雪明烛 本文关键词：LeetCode，力扣，算法，算法题，滑动窗口，中位数，multiset，刷题群

---

@TOC

题目地址：https://leetcode.com/problems/sliding-window-median/

题目描述

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples:

[2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Your job is to output the median array for each window in the original array.

For example,

Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.

Window position                Median
---------------               -----
[1  3  -1] -3  5  3  6  7       1
 1 [3  -1  -3] 5  3  6  7       -1
 1  3 [-1  -3  5] 3  6  7       -1
 1  3  -1 [-3  5  3] 6  7       3
 1  3  -1  -3 [5  3  6] 7       5
 1  3  -1  -3  5 [3  6  7]      6
Therefore, return the median sliding window as [1,-1,-1,3,5,6].

Note:

1. You may assume k is always valid, ie: k is always smaller than input array's size for non-empty array.

题目大意

求一个滑动窗口的中位数。

解题方法

MultiSet 遍历到中位数位置

这个题是239. Sliding Window Maximum的变形。

题目的意思很简单，要求滑动窗口中的元素的中位数。如果是求平均数，就简单很多了：每次滑动窗口移动，都是增加一个元素、删除一个元素，因此窗口内元素的 和 是非常好维护的，再除以窗口的大小就能得到平均数。

中位数 是有序序列最中间的那个数。也就是说我们必须对窗口内的元素「排序」。我们知道排序的时间复杂度一般是 O(k * log(k)) ，还是比较高的。这个题如果对每个区间都进行分别排序肯定会超时，否则也不会是个 Hard 题目。

怎么快速求中位数呢？为了降低时间复杂度的一个绝招就是增加空间复杂度：利用更好的数据结构。是的，我们的目的是快速让一组数据有序，那就寻找一个内部是有序的数据结构呗！下面我分语言讲解一下常见的内部有序的数据结构。

1. 在 C++ 中 set/multiset 是有序的集合，它们是基于红黑树实现的。其中 set 会对元素去重，而 multiset 可以有重复元素。

2. 在 Java 中 TreeSet 是有序的集合，它也是基于红黑树实现的。 TreeSet 会对元素去重。

3. 在 Python 中 heapq 实现了堆的算法，它不会对元素去重。

下面这个图是 C++ 的 multiset 内部结构示意图，它是个平衡二叉搜索树(BST)，插入元素时会自动调整二叉树，使得每个子树根节点的键值大于左子树所有节点的键值，同时保证根节点左右子树的高度相等。这样二叉树高度最小，检索速度最快。它的中序遍历是有序的，另外它也允许出现重复的值。

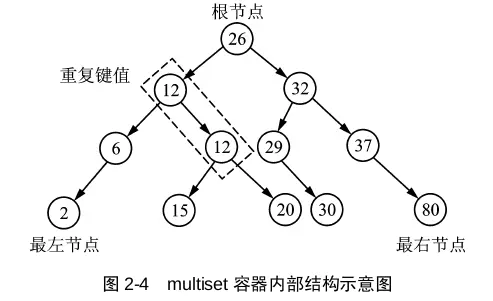
当频繁的插入和删除元素时，这些有序的数据结构能够在在 O(log(k)) 的时间复杂度内维护结构的有序性。但是对于红黑树实现的数据结构来说，不能做随机读取，因此获取中位数的时候，也只能通过 O(k) 时间复杂度的查找。

有了非常高效的数据结构，做这个题已经不难了。我下面的代码演示了用 C++ 的 multiset 解决本题。代码不长，但是需要对 C++ 的 stl 有一些了解。

1. 首先定义了结果数组 res 和 multiset；
2. 遍历输入中的每个元素；
3. 如果 multiset 中的元素超过了 k 个，需要把滑动窗口最左边 i - k 位置元素从 multiset 中删除（multiset 自动维护有序性）；
4. 把遍历到的当前元素插入到 multiset 中（multiset 自动维护有序性）；
5. 如果当前的位置达到了下标 k - 1，说明滑动窗口中有 k 个元素，开始求滑动窗口的中位数。

我们知道，如果数组 A 长度 k 是奇数时，令 mid = k / 2 ，那么中位数元素是 A[mid] ；如果数组长度 k 为偶数时，那么中位数是 (A[mid] + A[mid - 1]) / 2 。为了适应奇数和偶数长度，可以用通用的表达式 (A[mid] + A[mid - (1 - k % 2)]) / 2来求中位数。

求 multiset 里的中位数：我们先求 multiset 中所有元素的起始位置（最小元素），然后在此基础上让指针走 k / 2 步得到 mid ，最终 (A[mid] + A[mid - (1 - k % 2)]) / 2 就是我们要求的中位数。

时间复杂度： O(N*(log(k) + k)) ， log(k) 每次插入和删除操作， k 是找中位数操作。

C++ 代码如下：

class Solution {
public:
    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        vector<double> res;
        multiset<double> st;
        for (int i = 0; i < nums.size(); ++i) {
            if (st.size() >= k) st.erase(st.find(nums[i - k]));
            st.insert(nums[i]);
            if (i >= k - 1) {
                auto mid = st.begin();
                std::advance(mid, k / 2);
                res.push_back((*mid + *prev(mid, (1 - k % 2))) / 2);
            }
        }
        return res;
    }
};

MultiSet维护中位数指针

参考了grandyang大神的做法，维护中位数指针，这个中位数指针指向奇数区间的正中间或者偶数区间中间靠右的位置(e.g. [1,2,3,4]中的3)。既然每次会插入和删除元素各一个数字（总区间长度不变）：当插入一个数字时，如果这个数字比中位数小，则中位数左边的数字变多，那么把中位数指针向左边移动一个位置；当删除一个数字时，如果小于等于中位数（这里的等于是因为可能中位数被删除），则中位数左边的数字变少，那么把中位数指针向右边移动一个位置。

为什么只比较小于等于中位数，不判断当插入和删除的数字大于中位数时要如何移动指针呢？这个和我们每次插入和删除各一个数字有关，如果插入和删除都是比中位数大的，那么中位数不用动；如果插入和删除都是比中位数小的，那么中位数向左一步向右一步也没变；如果插入和删除一个比中位数大一个比中位数小，那么中位数正好按照两个if中的一个移动一个位置，仍然指向中位数。

C++代码如下，时间复杂度是O(N)，明显比上面的做法要快。

class Solution {
public:
    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        vector<double> res;
        multiset<double> st(nums.begin(), nums.begin() + k);
        auto mid = next(st.begin(), k / 2);
        for (int i = k; ;++i) {
            res.push_back((*mid + *prev(mid, 1 - k % 2)) / 2);
            if (i == nums.size()) return res;
            st.insert(nums[i]);
            if (nums[i] < *mid) --mid;
            if (nums[i - k] <= *mid) ++mid;
            st.erase(st.lower_bound(nums[i - k]));
        }
        return res;
    }
};

参考资料：https://www.cnblogs.com/grandyang/p/6620334.html

日期

2019 年 9 月 14 日 —— 假期的生活就是不规律 2021 年 2 月 3 日 —— 坚持日更公众号10天了！