505. The Maze II 迷宫 II
- 作者: 负雪明烛
- id: fuxuemingzhu
- 个人博客:http://fuxuemingzhu.cn/
@TOC
题目地址:https://leetcode-cn.com/problems/the-maze-ii/
题目描述
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the ball's start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
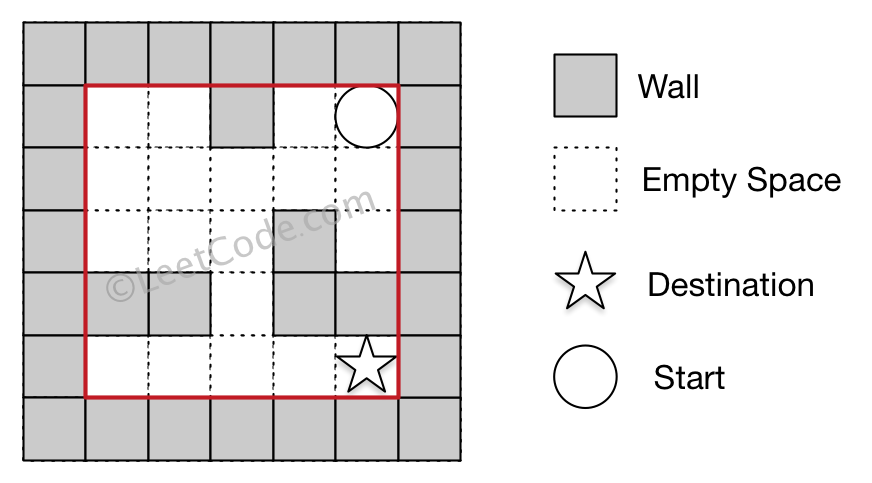
Example 1:
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)
Output: 12
Explanation: One shortest way is : left -> down -> left -> down -> right -> down -> right.
The total distance is 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.
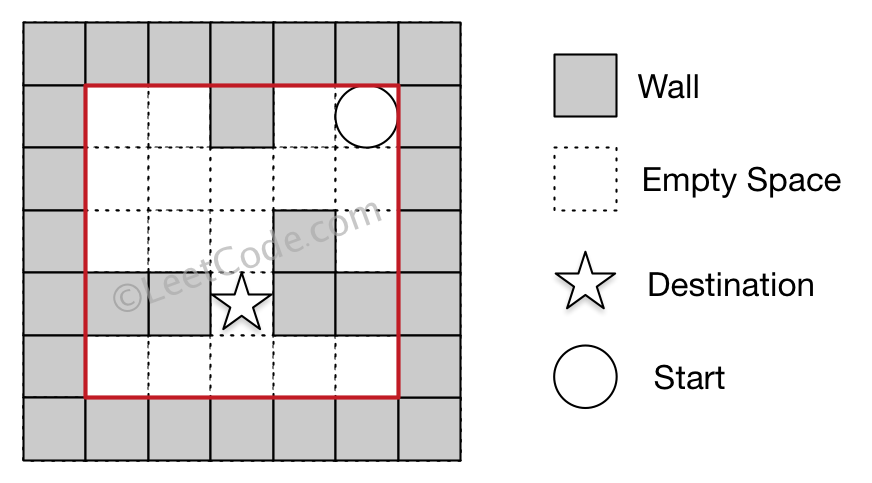
Example 2:
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)
Output: -1
Explanation: There is no way for the ball to stop at the destination.
Note:
- There is only one ball and one destination in the maze.
- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.
题目大意
小球可以向某个方向一直滚动,当撞到边缘或者墙壁时才停止,每次停止时才可以选择下个移动的方向。问小球是否能从起点出发恰好停在目的地,并返回小球滚动到目的地需要的最少步数。
解题方法
BFS
题目要我们求最少的移动步数,很显然我们使用BFS解决。一般的迷宫问题只会移动一个格子,但是这个题目要求我们撞到墙壁才停止,所以我们需要遍历四个方向,判断四个方向分别撞到墙壁时移动的步数和结束位置。当小球移动到该结束位置总的步数比历史上所有的位置都小,该结束位置放入队列中。
一般BFS需要有个visited数组,用来判断每个位置是否访问过,从而判断新位置是否加入队列中。但是这个题目不需要,因为只有当到达一个结置位置总的步数比以前到达这个位置的步数小的时候,才会加入队列,所以是有限制条件的,结果会是有限的,不会无限循环下去。
代码里使用了dp作为访问每个位置的最小步数,默认是INT_MAX。从起点开始,计算出小球能访问到的所有位置,直至再运动已经不能让所有可以停止的点的访问步数缩小时停止。最后返回结束位置的步数。
C++代码如下:
class Solution {
public:
int shortestDistance(vector<vector<int>>& maze, vector<int>& start, vector<int>& destination) {
const int M = maze.size();
const int N = maze[0].size();
vector<vector<int>> dp(M, vector<int>(N, INT_MAX));
queue<vector<int>> que;
que.push(start);
dp[start[0]][start[1]] = 0;
int count = 0;
while (!que.empty()) {
int size = que.size();
vector<int> start = que.front(); que.pop();
for (auto dir : dirs) {
vector<int> end(2, 0);
int step = rolling(maze, dir, start, end);
if (dp[end[0]][end[1]] > dp[start[0]][start[1]] + step) {
dp[end[0]][end[1]] = dp[start[0]][start[1]] + step;
que.push(end);
}
}
}
return dp[destination[0]][destination[1]] == INT_MAX ? -1 : dp[destination[0]][destination[1]];
}
private:
vector<vector<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int rolling(vector<vector<int>>& maze, vector<int>& curdir, vector<int>& start, vector<int>& end) {
end = start;
int step = 0;
while (true) {
int nxt_x = end[0] + curdir[0];
int nxt_y = end[1] + curdir[1];
if (nxt_x < 0 || nxt_x >= maze.size() || nxt_y < 0 || nxt_y >= maze[0].size()
|| maze[nxt_x][nxt_y] == 1) {
break;
}
end[0] = nxt_x;
end[1] = nxt_y;
step ++;
}
return step;
}
};
参考资料:https://leetcode-cn.com/problems/the-maze-ii/solution/c-bfs-by-sheng-ben-xin/
日期
2019 年 9 月 20 日 —— 是选择中国互联网式加班?还是外企式养生?
