790. Domino and Tromino Tiling 多米诺和托米诺平铺

作者： 负雪明烛 id： fuxuemingzhu 个人博客： http://fuxuemingzhu.cn/

---

题目地址: https://leetcode.com/problems/domino-and-tromino-tiling/description/

题目描述：

We have two types of tiles: a 2x1 domino shape, and an "L" tromino shape. These shapes may be rotated.

XX  <- domino

XX  <- "L" tromino
X

Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.

(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)

Example:

Input: 3
Output: 5
Explanation: 
The five different ways are listed below, different letters indicates different tiles:
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY

Note:

1. N will be in range [1, 1000].

题目大意

有个2N的长条，在里面堆放两种骨牌：一种是12的长方形，另一种是L形的，均有无限多个。问总的有多少种堆叠方式。

解题方法

看到要模一个数，说明结果很大，肯定需要使用DP求解。这个DP的转移方程不好找。下面的分析来自花花酱，

先找一下规律，如果只有一种长方形的长条的话，那么递推公式是这样的：

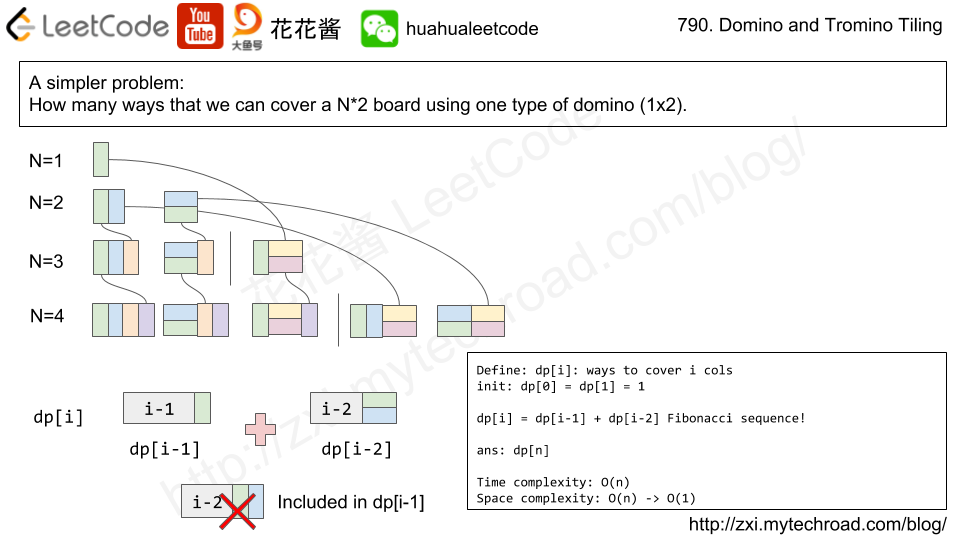
当有两种长条的时候，同样的道理能得到这种状态的递推公式。

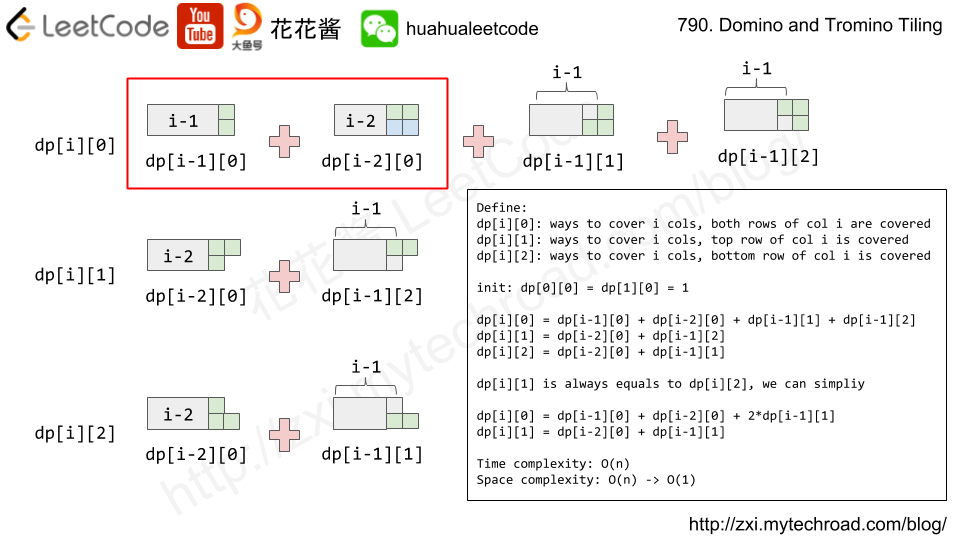
更详细的讲解要看花花酱的视频，我就不班门弄斧了。

时间复杂度是O(N)，空间复杂度是O(N)。

class Solution:
    def numTilings(self, N):
        """
        :type N: int
        :rtype: int
        """
        dp = [[0] * 2 for _ in range(N + 1)]
        dp[0][0] = 1
        dp[1][0] = 1
        for i in range(2, N + 1):
            dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + 2 * dp[i - 1][1]) % (10 ** 9 + 7)
            dp[i][1] = (dp[i - 2][0] + dp[i - 1][1]) % (10 ** 9 + 7)
        return dp[-1][0]

参考资料：

https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-790-domino-and-tromino-tiling/ https://www.youtube.com/watch?v=S-fUTfqrdq8

日期

2018 年 10 月 15 日 —— 美好的周一怎么会出现雾霾呢？