952. Largest Component Size by Common Factor 按公因数计算最大组件大小

作者： 负雪明烛 id： fuxuemingzhu 个人博客： http://fuxuemingzhu.cn/

---

@TOC

题目地址：https://leetcode.com/problems/largest-component-size-by-common-factor/description/

题目描述

Given a non-empty array of unique positive integers A, consider the following graph:

• There are A.length nodes, labelled A[0] to A[A.length - 1];
• There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1. Return the size of the largest connected component in the graph.

Example 1:

Input: [4,6,15,35] Output: 4

Example 2:

Input: [20,50,9,63] Output: 2

Example 3:

Input: [2,3,6,7,4,12,21,39] Output: 8

Note:

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= 100000

题目大意

如果两个数有公因子，就把他们链接到一起。问最大的一条链上面有多少个元素。

解题方法

并查集

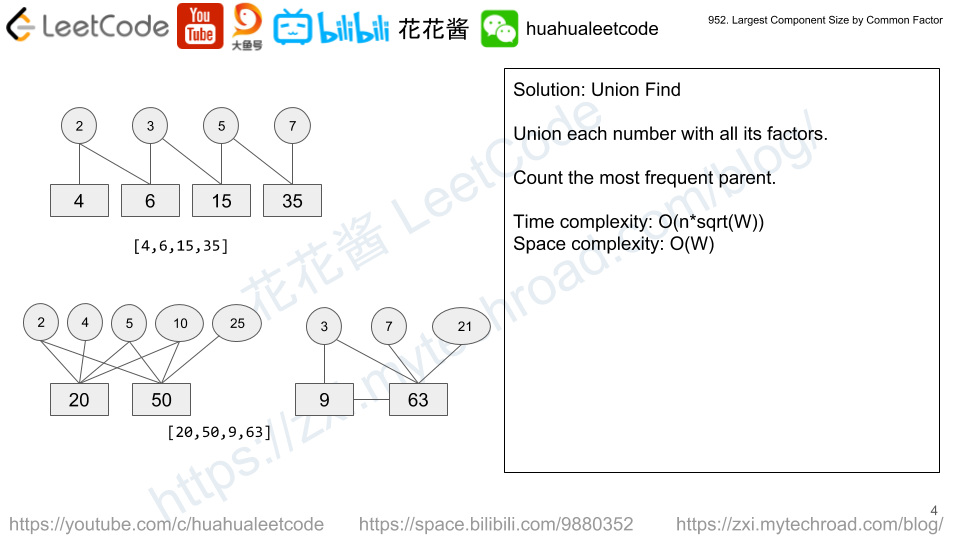
虽然这个题是hard题目，但是如果想明白了，很简单。任何两个数之间有相同的因子，就连接到一起，换句话说，可以把每个数字和它的所有因子进行链接，最后统计哪个因子上面的数字最多即可。

所以使用的方法是并查集，但是并不是把数组里面的两个元素进行合并，而是把每个数字和它所有的因子进行union。最后统计的数字也是某个因子上面的链接的数字的个数，因为这就是一条链的意思。

Python语言的效率比较慢，需要在find()的时候，做一次路径压缩。

class Solution:
    def largestComponentSize(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        ma = max(A)
        N = len(A)
        m = list(range(ma + 1))
        for a in A:
            for k in range(2, int(math.sqrt(a)) + 1):
                if a % k == 0:
                    self.u(m, a, k)
                    self.u(m, a, a // k)
        count = collections.defaultdict(int)
        for a in A:
            count[self.f(m, a)] += 1
        return max(count.values())
        
    def f(self, m, a):
        while m[a] != a:
            m[a] = m[m[a]]
            a = m[a]
        return a
    
    def u(self, m, a, b):
        if m[a] == m[b]: return
        pa = self.f(m, a)
        pb = self.f(m, b)
        m[pa] = pb

但是，C++的并查集不需要太对的路径压缩。效率快就是好。C++代码如下：

class Solution {
public:
    int largestComponentSize(vector<int>& A) {
        int mn = *max_element(A.begin(), A.end());
        m_ = vector<int>(mn + 1, -1);
        for (int i = 0; i < mn; i++) {
            m_[i] = i;
        }
        const int N = A.size();
        for (int a : A) {
            for (int i = 2; i <= sqrt(a); i++){
                if (a % i == 0) {
                    u(a, i);
                    u(a, a / i);
                }
            }
        }
        unordered_map<int, int> count;
        for (int a : A) {
            count[f(a)] ++;
        }
        int res = 0;
        for (auto c : count) {
            res = max(res, c.second);
        }
        return res;
    }
private:
    vector<int> m_;
    vector<int> rank;
    int f(int a) {
        if (m_[a] == a)
            return a;
        m_[a] = f(m_[a]);
        return m_[a];
    }
    void u(int a, int b) {
        int pa = f(a);
        int pb = f(b);
        if (pa != pb) {
            m_[pa] = m_[pb];
        }
    }
};

日期

2018 年 12 月 15 日 —— 今天四六级